Hey alle sammen!
Vil høre, om der er nogen, der kan hjælpe med en opgave:
Et dansk undersøgelse (n=100) viser at populationens gennemsnit har 95 % sikkerhedsinterval [8,2 - 10,5 ]. En tilsvarende svensk undersøgelse (n=50) resulterede i et 95 % sikkerhedsinterval [7,9 - 11,3].
Lav et t-test der belyser forskellen på svenskere og danskere.
Jeg har selv forsøgt at løse opgaven, men det virker ikke til at være det rigtige svar, jeg har.
Tak på forhånd!
Jeg må indrømme at have lidt erfaring med uparrede stikprøver, men hvor intet vover…! Jeg gør det sikkert mere besværligt end nødvendigt er.
Prøv at se http://statnoter.biolyt.dk/index.php?pageID=19 for hjælp
Først undersøges det med en F-test - se http://statnoter.biolyt.dk/index.php?pageID=29 om spredningerne er sammenlignelige:
Danske middeltal: 9,35
t(0,05)(49) = 2,010
Svensk middeltal: 9,6
t(0,05)(99) = 1,984
Vi har et tal for konfidensintervallet som beregnes ifølge
Denne anvender vi nu til at isolere SD fra testene ved at anvende den højeste grænse for konfidensintervallene
SD Dansk: 10,5 = 9,35 + 2,010 * SD/KVROD(100)
SD Dansk = (10,5-9,35)*KVROD(100)/2,010 = 5,721
SD Svensk: 11,3 = 9,6 + 1,984 * SD/KVROD(50)
SD Svensk = (11,3-9,6)*KVROD(50)/1,984 ) = 6,059
F-værdi udregnes ifølge F= SD[sub]1[/sub][sup]2[/sup]/SD[sub]2[/sub][sup]2[/sup] = 1,112
Helt indenfor F-tabelgrænser, der er varianshomogenitet og h0 accepteres!
Nu kan vi lave en t-testen med den viden at vi skal anvende formler for to teste med varianshomogenitet, først udregner vi SD:
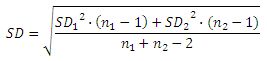
SD = KVROD(5,721[sup]2[/sup](100-1)+6,059[sup]2[/sup](50-1))/(100+50-2) = 5,835
Dette kan vi nu bruge i udregning af t-værdien:
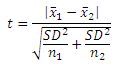
(9,6-9,35)/KVROD(5.835[sup]2[/sup]/100+5,835[sup]2[/sup]/50) = 0,247
t-værdien sammenlignes med tabelværdien, hvor antallet af frihedsgrader i en prøve med varianshomogenitet er n[sub]1[/sub]+n[sub]2[/sub]-2, altså 148.
t[sub]0,05/sub = 1,655
Siden at t[sub]test[/sub] < t[sub]tabel[/sub] accepteres h[sub]0[/sub]. Der er ud fra denne undersøgelse ikke signifikant forskel på målingerne af danskere og svenskere!
Dette fremgår også umiddelbart ud fra det store overlap i konfidensintervallerne og de store spredninger i undersøgelsen.
jeg har læst 3omnattens svar, og det lader til at være korrekt 
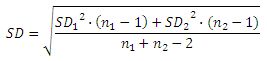
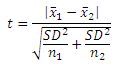
Nu er det dog lang tid siden, jeg har arbejdet med ssh.regning.
x med en streg ovenpå og betegner gennemsnittet af x, ikke? for ellers giver det ikke mening